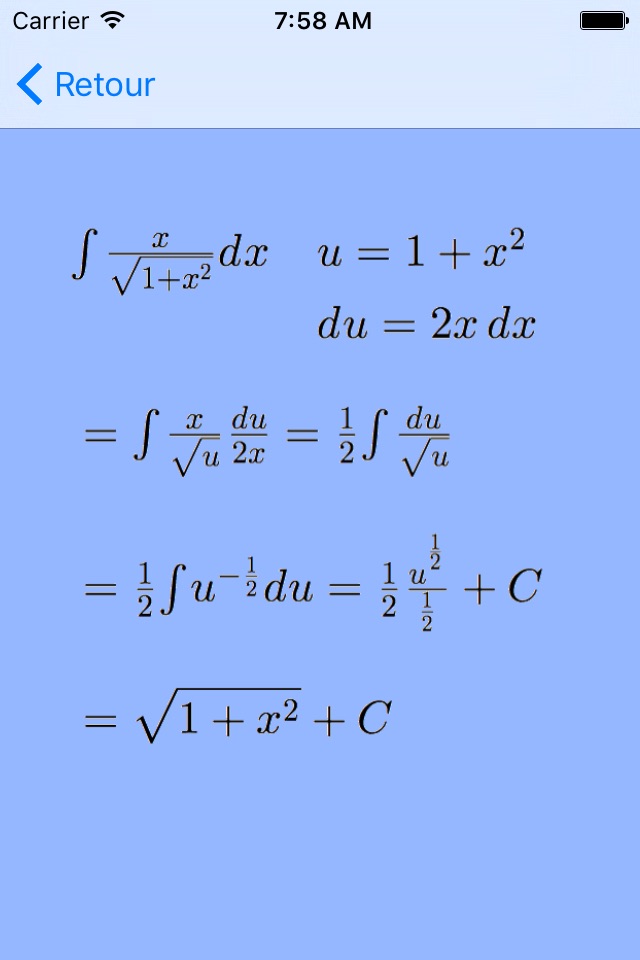Integrals trainer app for iPhone and iPad

Ever had an integral to solve and been wondering what is the best technique to use? Ever worked on a integral for long minutes, just to figure out you initially chose the wrong path? With this application, you can now concentrate on that critical first step: deciding what method to use! Look at an integral, choose what you would do, try again until you get it right, then go straight to the next integral! If need be, you can stop to look at a partial (sometimes complete) solution highlighting the first few steps of the resolution.

You will soon know, at a glance, what method to use to solve any reasonable integral! By becoming an expert at this critical first step, youll save time and get better grades!

The methods covered in this application are:

- Basic integrals, for the ones so simple that you can just give the answer right away.
- Separating integrals, when the integral becomes easier by solving many smaller ones.
- Substitution, when you let u=something to make the integral simpler.
- Partial fractions, when you rewrite your equation as a sum of smaller ones.
- Trigonometric identities, when you can use identities to simplify your integral.
- Triangle, when nothing simpler works and you willingly insert some trigonometry into your integral by use of a triangle.
- By parts, when you have two different families of functions in your integral.